Hexagonal lattice comprising of point masses interacting with axial and torsional springs. When boundary nodes are subjected to an affine deformation, the resulting displacement field can exhibit features ranging from uniform to localized deformation. These lattices have immense potential for wave steering applications.


Distinct patterns can form depending on the imposed boundary conditions, ranging from globally uniform patterns to localized deformation zones.
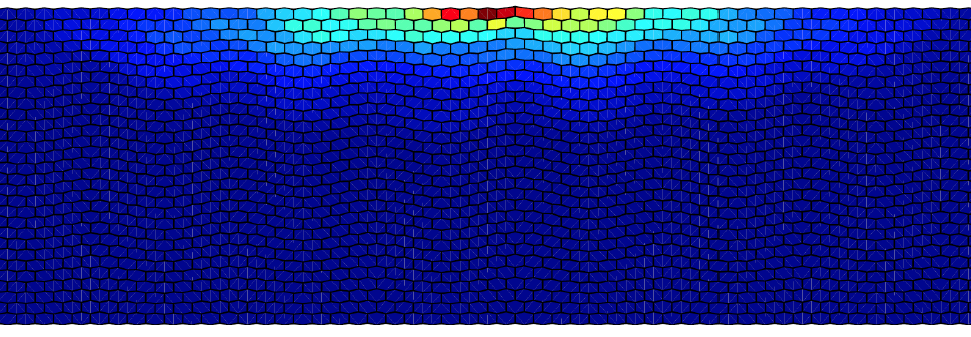
Such patterns can be viewed as instabilities and they can significantly change the effective physical properties. Here is an example of exploiting this change for tunable wave propagation, from isotropic to strongly directional (patterns form in lattice on right after compression)

Journal Publications:
- A study of deformation localization in nonlinear elastic square lattices under compression. Philosophical Transactions of the Royal Society A, 2018. R. K. Pal, F. Bonetto, L. Dieci and M. Ruzzene. pdf
- A continuum model for nonlinear lattices under large deformations. International Journal of Solids and Structures, 2016. R. K. Pal, M. Ruzzene and J. Rimoli. pdf
- Effect of large deformation pre-loads on the wave properties of hexagonal lattices. Smart materials and structures, 2015. R. K. Pal, J. Rimoli and M. Ruzzene. pdf